扩散模型应用·图生图与图像恢复

$$

封面来自 CivitAI.

图生图可以泛指基于输入图像生成新图像的过程，因此诸如 image restoration（超分、去噪、填充、上色等）、image-to-image translation、style transfer 等任务都可以归为其中。特别地，本文不包括基于文本的图像编辑方法，相关内容可在扩散模型应用·基于文本的图像编辑中查看。

SR3

Google TPAMI 2022 2021.04.15

SR3^[1] 将 DDPM 应用在了图像超分辨率中，取得了 SOTA 的效果。超分辨率是一种以低分辨率图像为条件的生成任务，把低分辨率图像融入模型的方式很简单——将其 bicubic 插值后 concatenate 到输入即可（作者也尝试了更复杂的，如 FiLM，但发现效果无明显差别）。另外，作者发现在 concatenate 之前做一些高斯模糊扰动能够有效提升 FID 2 个点。

与 DDPM 相比，SR3 做了一些有趣的改变。训练时，对于时间步 $$，DDPM 用的是 $$ 来计算相关变量和损失函数，但是 SR3 并没有直接使用 $$，而是从分布 $$ 之中随机取值；另外，模型直接接受 $$ 作为输入而非时间步 $$. 这些改变允许我们在 inference 时在一定范围内灵活地调整 noise scale 和采样步数，从而提高效率。

最后，论文中零散地提及了三个 future research，可供参考：

• 给前向过程加入条件
• 通过 $$ 来 scale 损失函数
• 引入类似于 BigGAN 的 quality-diversity trade-off，当然我们现在知道 classifier(-free) guidance 提供了一种解决方案。

点击查看 SR3 的生成样例（摘自论文）

SDEdit

Stanford CMU ICLR 2022 2021.08.02

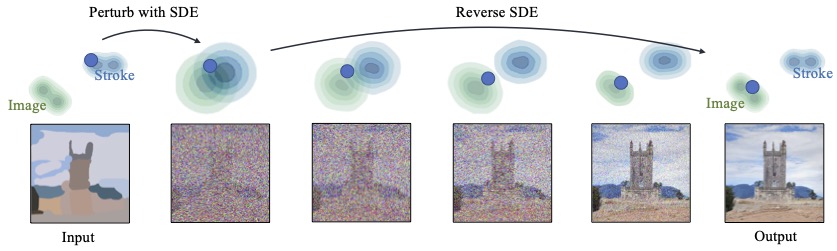
SDEdit^[2] 的思想一张图就能看明白：

真实图像和我们画的图像分属两个分布，我们通过前向加噪过程让两个分布的支撑集越来越大，直到产生交集就停下。从交集中的一点出发，用在真实图像上训练好的扩散模型逆向去噪，就回到了真实分布。

从图像处理的角度，我们知道加噪过程首先破坏的是高频信息，然后才破坏低频信息。所以当我们加噪到一定程度时，就可以去掉不想要的细节纹理，但仍保留大体结构，于是生成出来的图像就既能遵循输入的引导，又显得真实。

显然，这里一个关键问题就是在什么时候停止加噪。如果停的太早，那么结果不够真实；如果停的太晚，那么可能丢掉了我们想要的引导。论文里称之为 realism-faithfulness trade-off.

遗憾的是，这个问题没有一个通用的解答。它跟用户究竟想要更真实还是更还原有关，还跟引导图像本身的质量有关——如果引导图像是一片白色，那怎么着也没法很还原。一般而言，作者说在 $$ 区间内应该都还行（设时间是从 $$ 到 $$）。

点击查看 SDEdit 的生成样例（摘自官网）

ILVR

ICCV 2021 (oral) 2021.08.06

给定一张参考图像 $$，ILVR^[3] 通过精调 DDPM 逆向过程的每一步，让生成的图像 $$ 接近参考图像。所谓接近，即作者希望 DDPM 能够满足： $$ 其中 $$ 是一个低通滤波器，将输入图像下采样 $$ 倍后上采样回来（我们知道下采样会丢失图像的细节，即高频信息，所以操作后的图像只剩下了低频信息，是谓低通滤波）；$$ 是参考图像的加噪版本。上式的意义很明显：希望生成图像的低频信息与参考图像的低频信息相同。为了做到这一点，作者设计了如下逆向过程算法：

可以看到，在 DDPM 给出的 $$ 的基础上，作者加上了一个偏移量 $$. 假若上/下采样是最近邻插值，那么 $$，则： $$ 即满足了条件。作者尝试了不同的上/下采样方法，发现效果其实差不多。

下采样率 $$ 是一个超参数，$$ 越小，保留细节越多，生成图像就越接近参考图像。作者还指出，我们不一定在整个逆向过程都用到参考图像，可以只选择某些步用。选的步数越多，留给随机采样的发挥空间就越少，生成图像也越接近参考图像。

ILVR 与 classifier guidance 的联系

是否有人觉得，ILVR 似曾相识？没错，ILVR 和 classifier guidance 的本质是一样的！

• ILVR：对采样的结果偏移了 $$；
• Classifier guidance：对采样分布的均值偏移了 $$.

一方面，偏移结果（先采样再偏移）和偏移均值（先偏移再采样）显然是等价的；另一方面，$$ 大致是 $$ 到 $$ 方向的向量，朝该方向走能够提升 $$，这与 $$ 的意义相吻合。

更有甚者，二者都有一个控制引导强度的超参数：下采样率 $$ 和 guidance scale $$. 当 $$ 增大时，满足 $$ 的 $$ 更多，相当于 $$ 分布变得更平缓，引导作用更弱；而 $$ 减小时，$$ 也是变得更平缓，引导作用也是更弱。完美！

事实上，后文的许多工作都可以与 classifier guidance 建立起类似的联系。这类方法的特点是无需训练，只需要加载预训练模型，对逆向采样过程施加引导即可，对算力要求十分友好。

ILVR 可以有许多有趣的应用，比如给一个在狗上面训练的模型以猫作为参考图像，并合理控制 $$，那么模型就会生成像这只猫的狗；又比如我们对图像做一些粗糙的涂改后当作参考图像，合理控制 $$ 和步数范围，就能让模型既保留原有细节、又和谐化涂改的地方。

点击查看 ILVR 的生成样例（摘自论文）

Palette

Google SIGGRAPH 2022 2021.11.10

Palette^[4] 是 Google 提出的基于扩散模型做 Image-to-Image Translation 的统一框架，并分别在 colorization, inpainting, uncropping (outpainting) 和 JPEG restoration 四个任务上做了实验。Palette 并没有对不同任务做特别的调参、定制网络架构或任何辅助的损失，事实上，它也没对扩散模型做什么特别的改变，仅仅是把不同任务的退化后的图像当作条件给到模型而已。可能唯一需要提一下的就是对于 inpainting 和 uncropping (outpainting)，作者没有把 binary mask 给到模型，而是把缺失区域填上 Gaussian noise，这样的设置与扩散模型更搭。

作者做了两方面的 ablation study：

1. 常用 U-Net 架构里面的 (global) self-attention 真的有用。作者实验对比了 local self-attetion、无 attention 但用 dilated convolution、无 attention 但叠双倍的 resnet blocks，最后还是发现沿用 DDPM 就有的 attention 层最管用。
2. 许多基于扩散模型的图像恢复或翻译任务都采用的是 L1 loss 而非 L2 loss（如上文的 SR3 就用的 L1），作者实验发现二者的采样质量差不多，但是 L2 loss 能给出更多样的结果。推测是 L1 loss 倾向于让模型丢掉更多的模式。

点击查看 Palette 的生成样例（摘自官网）

RePaint

CVPR 2022 2022.01.24

RePaint^[5] 是专注于 image inpainting 任务的模型，其基本思想与Blended Diffusion^[6] 的 mask guidance 是一样的，即对于采样过程的每一步，掩码内使用模型的预测结果，而掩码外使用真实图像的加噪结果，如下图所示：

然而，上述采样模式会导致一个严重的问题——mask 内填充的内容与 mask 外已知的内容在语义上不能很好地匹配。这是因为针对已知部分的加噪过程并没有考虑 mask 内生成的部分。尽管在下一步模型会试图和谐化上一步的结果，但它本身又会带来的新的不和谐，所以这个问题会一直存在。更有甚者，我们的 noise level 是逐渐减小的，所以越往后越难更正前面各步带来的不和谐。

但是，考虑到 DDPM 的机制是生成符合数据分布的图像，它理应收敛到语义匹配的结果上，只是实际采样时每一步都引入的不和谐让收敛过程变得很慢。为此，作者提出了 resampling 技术，即不断地把生成的 $$ 重新扩散回 $$，在马尔可夫链上“反复横跳”，以期模型能缓解不和谐之处。当然，往回走一步可能不够，作者引入了两个超参数：$$ 表示每次往回走的步数，$$ 表示往回走多少次。下图是 $$ 下时间步的变化情况：

每一个尖峰高度是 j=10，每一段有 r=10 个尖峰。

显然，resampling 的代价就是采样时长变成了原本的 $$ 倍。

相比传统的基于 Auto-Encoder + GAN 的模型，基于扩散模型的 RePaint 有一个显著的优势：仅一个预训练模型就能无缝适配任意形状的 mask. 这是因为 RePaint 只改动了扩散模型的采样过程，不必专门为填充任务训练。作者尝试了几种不同的 mask 设置：Wide、Narrow、SR 2x、Alt. Lines 、Expand、Half，都取得了不错的效果。

点击查看 RePaint 的生成样例（摘自官方 repo）

DDRM

2022.01.27

DDIB

ICLR 2023 2022.05.16

DDIB^[8] 的理论写得非常 fancy，联系了 Schrödinger Bridge Problem、Optimal Transport 等理论知识，但其实做法很简单——把两个分别训练的 DDIM 用 latent space 连接起来，就可以完成 image-to-image translation 了，如下图所示：

具体而言，设有两个分别在源域 A 和目标域 B 上预训练好的扩散模型，输入一张域 A 的图像，DDIB 首先在第一个扩散模型上用 ODESolver（如 DDIM）把输入图像转换为隐变量，再在第二个扩散模型上用 ODESolver（如 DDIM）把该隐变量转换到域 B，就完成了域 A 到域 B 的迁移。

尽管 DDIB 非常直观简单，相比其他 image-to-image translation 方法，它有几个优点：

1. 具有 cycle consistency：$$，若忽略 ODESolver 的离散化误差，则 $$.
2. DDIB 用的两个扩散模型分别训练互不干扰，可以保证数据隐私性。
3. 如果要在 $$ 个域之间转换，只需要分别训练 $$ 个模型，而如 CycleGAN 需要两两训练 $$ 个模型。

但是，DDIB 毕竟没有显式地指导，所以转换过程也较难控制。特别地，当源域和目标域比较接近时（如狮子和老虎），DDIB 还能较好地工作；但是如果二者差距太大（如鸟和狗），那么源域图像中的主体的姿态就很难被保留下来。

点击查看 DDIB 的生成样例（摘自官网）

DDNM

PKU Shenzhen ICLR 2023 spotlight 2022.12.01

论文作者的知乎讲解：链接

在图像恢复任务中，超分、填充、上色对应的退化模式（下采样、掩码、灰度化）都属于线性退化，可以表达为如下形式： $$ 其中，$$ 是原图像，$$ 为退化矩阵，$$ 为退化图像。图像恢复就是已知 $$、$$，求 $$ 的过程（当然，在更难的盲图像恢复任务中，$$ 也是未知的）。

一般而言，同一个退化图像可以对应多个真实图像（称为 ill-posed problem），因此我们的目标其实是：

1. Consistency：求解 $$，使得 $$ 成立；
2. Realness：$$，其中 $$ 代表真实图像的分布。

为解决这个问题，论文作者首先指出了 range-null space decomposition. 设 $$ 的伪逆为 $$，即满足 $$，那么 $$ 可以分解为： $$ 其中第一项 $$ 是 $$ 的 range-space，因为 $$；而第二项 $$ 是 $$ 的 null-space，因为 $$.

将 range-null space decomposition 应用到图像恢复任务中，我们能直接构造出满足 consistency 的解： $$ 因为无论 $$ 是什么，都有： $$ 但是 $$ 会影响 realness. 所以我们现在希望找到 $$，使得 $$，这就是扩散模型的用武之地了。

我们知道，扩散模型在第 $$ 步会预测一个 "clean" image $$，但它并不一定满足 consistency. 为此，作者做出修改： $$ 那么根据上文所述，$$ 是一定满足 consistency 的；又由于 $$ 其实就是 $$，所以我们能保证生成的结果满足 consistency. 接下来用修改后的结果计算 $$： $$ 重复这个过程，算法和图示如下：

相比 DDPM，这里扩散模型只参与了 null-space 一项的计算，range-space 一项是我们直接计算的，所以作者将这种方法称为 Denoising Diffusion Null-Space Model (DDNM)^[9].

可以看到，DDNM 要求我们知道 $$ 和 $$. 那么对于常见的退化，它们的 $$ 可以构造为：

1. 填充：mask 就是 $$。又由于 $$，所以 $$；
2. 上色：$$，即将各通道数值做平均。其伪逆为 $$，可以由 $$ 验证；
3. 超分：与上色类似，取 $$，其中 $$ 是 patch 大小，好比 average pooling 层。其伪逆为 $$，好比 nearest upsample 层。
4. 复杂退化：以老照片修复为例，我们既需要填充划痕，又需要上色，还可能需要超分。因此 $$，对应伪逆为 $$.

DDNM 可以解决没有噪声干扰的图像恢复任务，但是不能很好地解决带噪声的任务。为此，作者提出了 DDNM+，做了两方面的改进：

1. 对于带噪声的任务，作者将其建模为： $$ 如果直接应用 DDNM，有： $$ 可以看见噪声 $$ 会被保留下来并传递给 $$，最终影响恢复效果。为了解决这个问题，考虑到扩散模型的逆向过程本身就是一个高斯分布，那么这个噪声 $$ 不正好可以利用进去吗？我们只需要调小方差，让 $$ 帮我们“补齐”调小的这一部分。于是，作者引入了两个参数 $$ 和 $$： $$ 特别地，如果取 $$，$$，代入上式并都展开： $$ 首先观察第一个式子，$$ 的随机性完全来自于第一项。考虑到在超分和上色中，$$ 都是复制操作，所以 $$ 依旧可以用 $$ 来近似，因此 $$.

   再看第二个式子，$$ 的随机性来自于第一项和第三项，为了方便叙述，记 $$ 前面那一坨系数为 $$，那么第一项的方差就是 $$；第三项方差显然是 $$. 二者独立因此方差可加，所以 $$.

   前文说过，我们引入两个参数是希望 $$ 补齐故意调小的方差，所以应该让 $$ 与 $$ 的方差相等，即 $$；另一方面，$$ 其实是有害于 consistency 的，所以我们应该尽可能让它接近 $$. 综上，作者最终选取： $$

2. Time-Travel Trick. 作者发现，在大规模 average pooling 的超分、大 mask 填充、低采样率的压缩感知场景下，DDNM 的效果并不好。这是因为 $$ 过于的 local，不能给逆向过程以有效的引导。作者给出的解决方案与 RePaint 的来回采样类似，即在 $$ 时刻往回采样 $$，然后重新执行 DDNM 直到得到 $$.

DDNM+ 的算法如下所示：

点击查看 DDNM 的生成样例（摘自官网）

References

1. Saharia, Chitwan, Jonathan Ho, William Chan, Tim Salimans, David J. Fleet, and Mohammad Norouzi. Image super-resolution via iterative refinement. IEEE Transactions on Pattern Analysis and Machine Intelligence (2022). ↩︎
2. Meng, Chenlin, Yutong He, Yang Song, Jiaming Song, Jiajun Wu, Jun-Yan Zhu, and Stefano Ermon. Sdedit: Guided image synthesis and editing with stochastic differential equations. In International Conference on Learning Representations. 2021. ↩︎
3. Choi, Jooyoung, Sungwon Kim, Yonghyun Jeong, Youngjune Gwon, and Sungroh Yoon. ILVR: Conditioning Method for Denoising Diffusion Probabilistic Models. In 2021 IEEE/CVF International Conference on Computer Vision (ICCV), pp. 14347-14356. IEEE, 2021. ↩︎
4. Saharia, Chitwan, William Chan, Huiwen Chang, Chris Lee, Jonathan Ho, Tim Salimans, David Fleet, and Mohammad Norouzi. Palette: Image-to-image diffusion models. In ACM SIGGRAPH 2022 Conference Proceedings, pp. 1-10. 2022. ↩︎
5. Lugmayr, Andreas, Martin Danelljan, Andres Romero, Fisher Yu, Radu Timofte, and Luc Van Gool. Repaint: Inpainting using denoising diffusion probabilistic models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 11461-11471. 2022. ↩︎
6. Avrahami, Omri, Dani Lischinski, and Ohad Fried. Blended diffusion for text-driven editing of natural images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 18208-18218. 2022. ↩︎
7. DDRM ↩︎
8. Su, Xuan, Jiaming Song, Chenlin Meng, and Stefano Ermon. Dual diffusion implicit bridges for image-to-image translation. In The Eleventh International Conference on Learning Representations. 2022. ↩︎
9. Wang, Yinhuai, Jiwen Yu, and Jian Zhang. Zero-Shot Image Restoration Using Denoising Diffusion Null-Space Model. arXiv preprint arXiv:2212.00490 (2022). ↩︎