2020-02-03发表2020-12-20更新ICPC/CCPC / Contests / Codeforces21 分钟读完 (大约3203个字)

Codeforces Round #616 (Div.2)

比赛链接 / 官方题解链接

A. Even But Not Even

Solution

从后往前删数直至满足题意或无解。

Better Solution

若奇数个数大于1，任意输出2个奇数；否则无解。

Code

>folded

#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>

using namespace std;

template<typename T>void read(T&x){x=0;int fl=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')
fl=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}x*=fl;}
template<typename T,typename...Args>inline void read(T&t,Args&...args){read(t);read(args...);}

const int N = 3005;

int T, n;
char s[N];

int main(){
    scanf("%d", &T);
    while(T--){
        scanf("%d", &n);
        scanf("%s", s+1);
        int len = strlen(s+1);
        while(len >= 1 && (s[len] - '0') % 2 == 0)  len--;
        if(len == 0){
            puts("-1");
            continue;
        }
        int sum = 0;
        for(int i = 1; i <= len; i++)   sum += s[i] - '0';
        if(sum % 2 == 0){
            for(int i = 1; i <= len; i++)   putchar(s[i]);
            putchar(10);
            continue;
        }
        int mark = 0;
        for(int i = len - 1; i >= 1; i--){
            if((s[i]-'0') & 1){
                mark = i;
                break;
            }
        }
        if(!mark){
            puts("-1");
            continue;
        }
        bool out = false;
        for(int i = 1; i < mark; i++)   out = true, putchar(s[i]);
        for(int i = mark + 1; i <= len; i++)    out = true, putchar(s[i]);
        if(!out)    printf("-1");
        putchar(10);
    }
    return 0;
}

B. Array Sharpening

Solution

若 $a_i\geq i-1$，且 $a_{i-1}$ 可作为递增数列的结尾，那么 $a_i$ 也可以作为递增数列的结尾；下降数列同理。若存在 $a_i$ 使得其既可作为递增数列的结尾，也可作为下降数列的开头，则输出 Yes；否则输出 No。

Code

>folded

#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>

using namespace std;

template<typename T>void read(T&x){x=0;int fl=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')
fl=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}x*=fl;}
template<typename T,typename...Args>inline void read(T&t,Args&...args){read(t);read(args...);}

typedef long long LL;

const int N = 300005;

int T, n;
LL a[N];
bool in[N], de[N];

int main(){
    scanf("%d", &T);
    while(T--){
        scanf("%d", &n);
        for(int i = 1; i <= n; i++){
            in[i] = de[i] = 0;
            read(a[i]);
        }
        for(int i = 1; i <= n; i++){
            if(a[i] >= i - 1)   in[i] = 1;
            else    break;
        }
        for(int i = n; i >= 1; i--){
            if(a[i] >= n - i)   de[i] = 1;
            else    break;
        }
        bool can = false;
        for(int i = 1; i <= n; i++){
            if(in[i] && de[i]){
                puts("Yes");
                can = true;
                break;
            }
        }
        if(!can)    puts("No");
    }
    return 0;
}

C. Mind Control

Solution

只用考虑排在你前面的人，$k$ 最大取到 $m-1$ 即可。假设受你控制的 $k$ 人中，有 $x$ 人取队首，$k-x$ 人取队尾；不受控制的 $m-1-k$ 人中，有 $y$ 人取队首，$m-1-k-y$ 人取队尾，则 $m-1$ 人取完后，还剩下 $[x+y+1,x+y+n-m+1]$ 区间的数，你取到的数是 $\max(a_{x+y+1},a_{x+y+n-m+1})$，于是可以枚举 $x,y$，记录最小的取到的数的最大值。

事实上，$ans=\max\limits_{x=0}^k\left[\min\limits_{y=0}^{m-1-k}\left[\max(a_{x+y+1},a_{x+y+n-m+1})\right]\right]$.

复杂度 $O(n^2)$

Advanced version

【参考官方题解】存在 $O(n)$ 的解法。对上面的式子变形：

$ans=\max\limits_{x=0}^k\left[\min\limits_{y=x}^{x+m-1-k}\left[\max(a_{y+1},a_{y+n-m+1})\right]\right]$

其中，$\max(a_{y+1},a_{y+n-m+1})$ 是可以 $O(1)$ 解得的，不妨记为 $b_y$，则

$ans=\max\limits_{x=0}^k\left[\min\limits_{y=x}^{x+m-1-k}b_y\right]$

于是可以枚举 $x$，同时维护一个单调（递增）队列，在线性时间内求解。

Code —- $O(n^2)$

>folded

#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>

using namespace std;

template<typename T>void read(T&x){x=0;int fl=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')
fl=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}x*=fl;}
template<typename T,typename...Args>inline void read(T&t,Args&...args){read(t);read(args...);}

typedef long long LL;

const int N = 3505;

int T, n, m, k, a[N];

inline int solve(int l, int r, int x){
    int res = 1e9;
    for(int i = 0; i <= x; i++){
        res = min(res, max(a[l + i], a[r - (x - i)]));
    }
    return res;
}

int main(){
    scanf("%d", &T);
    while(T--){
        read(n, m, k);
        k = min(k, m - 1);
        for(int i = 1; i <= n; i++) read(a[i]);
        int ans = 0;
        for(int i = 1; i <= n; i++){
            int j = i + n - k - 1;
            if(j > n)   break;
            ans = max(ans, solve(i, j, m - 1 - k));
        }
        printf("%d\n", ans);
    }
    return 0;
}

Code —- $O(n)$

>folded

#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>

using namespace std;

template<typename T>void read(T&x){x=0;int fl=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')
fl=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}x*=fl;}
template<typename T,typename...Args>inline void read(T&t,Args&...args){read(t);read(args...);}

typedef long long LL;

const int N = 3505;

int T, n, m, k, a[N];

inline int func(int y){ return max(a[y+1], a[n-m+1+y]); }

int main(){
    read(T);
    while(T--){
        int ans = 0;
        read(n, m, k);
        k = min(k, m - 1);
        for(int i = 1; i <= n; i++) read(a[i]);
        deque<int> q;
        for(int x = 0, j = 0; x <= k; x++){
            while(!q.empty() && q.front() < x)    q.pop_front();
            while(j <= m-1-k+x){
                while(!q.empty() && func(j) <= func(q.back())) q.pop_back();
                q.push_back(j);
                j++;
            }
            ans = max(ans, func(q.front()));
        }
        printf("%d\n", ans);
    }
    return 0;
}

D. Irreducible Anagrams

Solution

【参考官方题解】难点在于寻找 “字符串 $s$ 具有至少一个 irreducible anagram ” 的充要条件。充要条件是字符串 $s$ 满足下列条件之一：

$s.length()=1$
$s_1\neq s_n$
$s$ 含有至少三个不同字母

证明：易知条件1是充分条件；对于条件2，只需将所有 $s_n$ 字母放在最开头，那么容易知道，除了 $s$ 本身以外，$s$ 的其他所有前缀的 $s_n$ 字母出现次数不同于原次数，自然是一个 irreducible anagram，于是条件2也是充分条件。同时不满足条件1、2的字符串满足 $s_1=s_n$，将它们分为三类：

$s_1=s_n$ 且含至少三个不同字母：取最靠后一个不同于 $s_1$ 的字母（设为 $x$），把所有该字母放在开头，紧接着所有 $s_1$ 字母，那么每一个前缀要么有更多的 $x$，要么有更少的 $s_1$，是 irreducible anagram。
$s_1=s_n$ 且仅有两个不同字母：不妨设两个不同字母为 $a,b$，$s_1=s_n=a$，$s_x=s_y=b$ 且 $s_x$ 是第一个 $b$，$s_y$ 是最后一个 $b$。假设 $t$ 是 $s$ 的 irreducible anagram，则 $t_1=t_n=b$，于是 $t$ 的前 $x$ 位 $b$ 的次数比 $s$ 多，而前 $y$ 位 $b$ 的次数比 $s$ 少，那么存在一个 $z$，使得前 $z$ 位 $b$ 的次数相等，那么 $s[1…z],t[1…z]$ 是 anagram，因此不存在 irreducible anagram。
$s_1=s_n$ 且仅有一个字母：显然不存在。

证毕。

有了上述充要条件，这道题就很简单了。

Code

>folded

#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>

using namespace std;

template<typename T>void read(T&x){x=0;int fl=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')
fl=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}x*=fl;}
template<typename T,typename...Args>inline void read(T&t,Args&...args){read(t);read(args...);}

typedef long long LL;

const int N = 200005;

int q, l, r;
char s[N];

struct Node{
    int buc[30];
    Node() { memset(buc, 0, sizeof buc); }
}a[N];
Node operator + (const Node &A, const Node &B){
    Node C;
    for(int i = 0; i < 26; i++) C.buc[i] = A.buc[i] + B.buc[i];
    return C;
}
Node operator - (const Node &A, const Node &B){
    Node C;
    for(int i = 0; i < 26; i++) C.buc[i] = A.buc[i] - B.buc[i];
    return C;
}

int main(){
    scanf("%s", s+1);
    int len = strlen(s+1);
    for(int i = 1; i <= len; i++){
        a[i] = a[i-1];
        a[i].buc[s[i]-'a']++;
    }
    read(q);
    while(q--){
        read(l, r);
        if(l == r || s[l] != s[r])  puts("Yes");
        else{
            Node t = a[r] - a[l-1];
            int cnt = 0;
            for(int i = 0; i < 26; i++) cnt += (t.buc[i] > 0);
            if(cnt >= 3)    puts("Yes");
            else    puts("No");
        }
    }
    return 0;
}

E. Prefix Enlightenment

Solution

题目条件中“任意三个集合交集为空”可翻译为“任意一盏灯最多属于两个集合”，考虑每一盏灯，我们可以得到集合与集合之间的关系：

若灯属于两个集合 $A$ 和 $B$
- 若灯为开，则 $A,B$ 必须同时取或者同时不取
- 若灯为关，则 $A,B$ 取且仅取其一
若灯属于一个集合 $A$
- 若灯为开，则 $A$ 必不能取
- 若灯为关，则 $A$ 必须取
若灯不属于任何集合，直接跳过不作处理

只考虑灯属于两个集合的话，这就是一个种类并查集，拆点即可（$A$ 拆为 $A$ 和 $A+k$）。

然而对于 $A$ 必/必不取这种约束条件不好维护，一个巧妙的方法是：开一个大小记为 $+\infty$ 的点，那么对于 $A$ 必取的情况，把 $A+k$ 与之合并，则更新答案时一定是用 $A$ 更新的，达到了必取的效果；必不取同理。

Code

>folded

#include<algorithm>
#include<cstdio>
#include<vector>

using namespace std;

template<typename T>void read(T&x){x=0;int fl=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')
fl=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}x*=fl;}
template<typename T,typename...Args>inline void read(T&t,Args&...args){read(t);read(args...);}

typedef long long LL;

const int N = 300005;
const int INF = 1e9;

int n, k, c;
vector<int> vec[N];
char s[N];

int fa[N<<1], sz[N<<1];
inline int lowbit(int x){ return x & -x; }
inline int findfa(int x){ return x == fa[x] ? x : fa[x] = findfa(fa[x]); }
inline void unionn(int x, int y){
    x = findfa(x), y = findfa(y);
    fa[y] = x;
    if(sz[x] < INF) sz[x] += sz[y];
}

int main(){
    read(n, k);
    scanf("%s", s+1);
    for(int i = 1; i <= k; i++){
        read(c);
        for(int j = 1; j <= c; j++){
            int x; read(x);
            vec[x].push_back(i);
        }
    }
    for(int i = 1; i <= k * 2; i++) fa[i] = i, sz[i] = (i <= k);
    fa[k*2+1] = k*2+1, sz[k*2+1] = INF;
    int ans = 0;
    for(int i = 1; i <= n; i++){
        if(vec[i].size() == 1){
            if(findfa(k*2+1) != findfa(vec[i][0] + k * (s[i] == '0'))){
                ans -= min(sz[findfa(vec[i][0])], sz[findfa(vec[i][0]+k)]);
                unionn(k*2+1, vec[i][0] + k * (s[i] == '0'));
                ans += min(sz[findfa(vec[i][0])], sz[findfa(vec[i][0]+k)]);
            }
        }
        else if(vec[i].size() == 2){
            if(s[i] == '0'){
                if(findfa(vec[i][0]) != findfa(vec[i][1]+k)){
                    ans -= min(sz[findfa(vec[i][0])], sz[findfa(vec[i][0]+k)]);
                    ans -= min(sz[findfa(vec[i][1])], sz[findfa(vec[i][1]+k)]);
                    unionn(vec[i][0], vec[i][1]+k);
                    unionn(vec[i][0]+k, vec[i][1]);
                    ans += min(sz[findfa(vec[i][0])], sz[findfa(vec[i][0]+k)]);
                }
            }
            else{
                if(findfa(vec[i][0]) != findfa(vec[i][1])){
                    ans -= min(sz[findfa(vec[i][0])], sz[findfa(vec[i][0]+k)]);
                    ans -= min(sz[findfa(vec[i][1])], sz[findfa(vec[i][1]+k)]);
                    unionn(vec[i][0], vec[i][1]);
                    unionn(vec[i][0]+k, vec[i][1]+k);
                    ans += min(sz[findfa(vec[i][0])], sz[findfa(vec[i][0]+k)]);
                }
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

F. Coffee Varieties (easy version)

Solution

【参考官方题解】把长为 $n$ 的序列 $a$ 分成长度为 $\frac{k}{2}$ 的 $\frac{2n}{k}$ 块，块与块之间两两组合拿去询问，回答 Y 的打上标记即可。

正确性证明：对于任意一个不是第一次出现的数 $a_j$，假设 $a_i=a_j,i<j$，那么一定存在一次询问同时包含了 $a_i,a_j$，这个询问之后 $a_j$ 就被标记上了。

总询问次数 $=\frac{\frac{2n}{k}\cdot\left(\frac{2n}{k}-1\right)}{2}\cdot k=\frac{2n^2}{k}-n$.

Code

>folded

#include<algorithm>
#include<cstring>
#include<cstdio>

using namespace std;

template<typename T>void read(T&x){x=0;int fl=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')
fl=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}x*=fl;}
template<typename T,typename...Args>inline void read(T&t,Args&...args){read(t);read(args...);}

typedef long long LL;

const int N = 1100;

int n, k;

inline bool ask(int c){
    printf("? %d\n", c); fflush(stdout);
    char ch[2]; scanf("%s", ch);
    return ch[0] == 'N';
}
inline void reset(){ puts("R"); fflush(stdout); }

bool isFirst[N];

int main(){
    memset(isFirst, 1, sizeof isFirst);
    read(n, k);
    for(int len = 2; len <= 2 * n / k; len++){
        for(int i = 1; i <= 2 * n / k; i++){
            int j = i + len - 1;
            if(j > 2 * n / k)   break;
            for(int o = (i - 1) * k / 2 + 1; o <= i * k / 2; o++)
                if(ask(o) == false)
                    isFirst[o] = false;
            for(int o = (j - 1) * k / 2 + 1; o <= j * k / 2; o++)
                if(ask(o) == false)
                    isFirst[o] = false;
            reset();
        }
    }
    int cnt = 0;
    for(int i = 1; i <= n; i++) cnt += isFirst[i];
    printf("! %d\n", cnt); fflush(stdout);
    return 0;
}

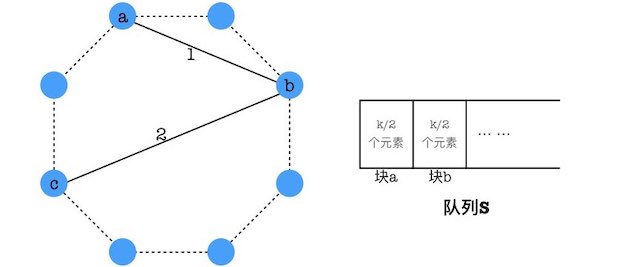
Div 1. D. Coffee Varieties (hard version)

Solution

【参考官方题解】沿袭 easy version 的思路，方便起见，记块数为 $m=\frac{2n}{k}$，如果把每一个块看成一个点，两两组合看成连边，则可以构建出一个 $K_m$ 完全图。在 easy version 中，我们事实上是把每条边拿出来进行询问，一共 $C_m^2$ 条边，每条边问 $k$ 次，故一共询问了 $k\cdot C_m^2$ 次。

但是如下图所示，当我们询问了边 $1$ 之后（即询问了块 $a,b$ 之后），如果我们紧接着询问边 $2$，那么块 $b$ 仍然存在于队列之中，没有必要将其再加进去，这就减少了询问次数。更一般地，只要我们询问的边依次形成一条简单路径，那么我们沿着这条路径询问即可。设路径长度为 $l$，那么上面有 $l+1$ 个点，每个点也即每个块有 $\frac{k}{2}$ 个元素，所以一条路径询问的次数就是 $(l+1)\cdot \frac{k}{2}$。我们的目标是找出多条边不同的简单路径，使之覆盖完全图 $K_m$ 的所有边。此时，设共有 $p$ 条路径，则询问次数为 $\sum\left((l_i+1)\cdot\frac{k}{2}\right)=(C_m^2+p)\cdot\frac{k}{2}$.

找路径的方法有很多，我采用的是枚举出发点，再枚举边的长度，画一条每条边长度相同的路径直至末尾。可以算得，这样 $p=\frac{m^2}{4}$，总询问次数为 $\frac{3n^2}{2k}-\frac{n}{2}$.

官方题解指出：实验中随机化 dfs 表现很好，大概是 $1.2\frac{n^2}{k}$ 次询问；还给出了一种 $\frac{n^2}{k}$ 次询问的方法。

Code

>folded

#include<algorithm>
#include<cstring>
#include<cstdio>

using namespace std;

template<typename T>void read(T&x){x=0;int fl=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')
fl=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}x*=fl;}
template<typename T,typename...Args>inline void read(T&t,Args&...args){read(t);read(args...);}

typedef long long LL;

const int N = 1100;

int n, k;

inline bool ask(int c){
    printf("? %d\n", c); fflush(stdout);
    char ch[2]; scanf("%s", ch);
    return ch[0] == 'N';
}
inline void reset(){ puts("R"); fflush(stdout); }

bool tag[N];

int main(){
    memset(tag, 1, sizeof tag);
    read(n, k);
    int m = 2 * n / k;
    for(int i = 1; i <= m / 2; i++){
        for(int gap = i; gap <= m - i; gap++){
            reset();
            int now = i;
            while(now <= m){
                for(int j = (now - 1) * k / 2 + 1; j <= now * k / 2; j++)
                    if(ask(j) == false) tag[j] = false;
                now += gap;
            }
        }
    }
    int cnt = 0;
    for(int i = 1; i <= n; i++) cnt += tag[i];
    printf("! %d\n", cnt); fflush(stdout);
    return 0;
}

Codeforces Round #616 (Div.2)

http://xyfjason.github.io/blog-xcpc/2020/02/03/Codeforces-Round-616-Div-2/

作者

xyfJASON

发布于

2020-02-03

更新于

2020-12-20

许可协议

#Codeforces

Codeforces Round #616 (Div.2)

A. Even But Not Even

Solution

Better Solution

Code

B. Array Sharpening

Solution

Code

C. Mind Control

Solution

Advanced version

Code —- $O(n^2)$

Code —- $O(n)$

D. Irreducible Anagrams

Solution

Code

E. Prefix Enlightenment

Solution

Code

F. Coffee Varieties (easy version)

Solution

Code

Div 1. D. Coffee Varieties (hard version)

Solution

Code

作者

发布于

更新于

许可协议

评论

分类

最新文章

标签